第 3 章 网络商品经济学入门

提示🎧 本章配套播客

当你考虑购买一袋土豆时，你不会关心其他消费者的选择——他们买不买土豆与你从这袋土豆中获得的效用毫无关系。但如果换成选择一款通讯软件呢？你会优先选择朋友们都在用的那款，因为只有当足够多的人使用同一款软件时，你才能与他们交流。这就是网络效应（Network Effects）改变经济分析的核心所在：用户的决策不再是独立的，而是相互依赖的。

前两章我们认识了平台的基本特征和运营机制，但还没有深入分析网络效应的数学结构。本章将填补这一空白。我们将建立严格的博弈论模型，揭示网络效应如何导致需求的相互依赖、多重均衡的存在，以及临界规模的关键作用。这些理论工具将为后续章节的平台定价、设计和竞争分析奠定坚实基础。

重要学习目标

1. 理解 网络效应如何使用户决策相互依赖，改变传统需求分析的逻辑
2. 掌握 满足预期均衡的概念，分析多重均衡和自我实现预期的机制
3. 运用 博弈论模型分析网络商品的定价决策和市场结构
4. 辨析 临界规模、市场倾覆与兼容性决策的经济逻辑

第3章思维导图

3.1 网络商品需求

网络商品（Network Goods）的需求分析与传统商品截然不同。在传统市场中，每个消费者可以独立决策——给定价格，判断商品价值是否超过价格即可。但在网络商品市场，你的购买决策取决于你对其他人购买决策的预期，而其他人的决策又取决于他们对你的预期。这种相互依赖使得需求分析变成了博弈论问题。

3.1.1 双用户简单模型

我们从最简单的情形开始：只有两个用户 Xena 和 Yuri，他们同时决定是否购买某个网络商品。

模型设定

两个用户对产品有不同的内在估值（Intrinsic Valuation）：\(r_x\) 和 \(r_y\)，假设 \(r_x > r_y\)（Xena 更看重这个产品）。产品价格为 \(A\)。如果两人都购买，每人还可以获得额外的网络收益（Network Benefit）\(\beta > 0\)——例如，两人都用 Dropbox，就可以共享文件夹。

用户的净收益取决于自己和对方的选择。我们可以用收益矩阵来表示这个博弈：

	Yuri 购买	Yuri 不买
Xena 购买	\(r_x + \beta - A\)，\(r_y + \beta - A\)	\(r_x - A\)，\(0\)
Xena 不买	\(0\)，\(r_y - A\)	\(0\)，\(0\)

这是一个典型的协调博弈（Coordination Game）。让我们寻找纳什均衡。

均衡分析

1. 双方都购买是均衡，当且仅当双方都不想单方面偏离：\(r_x + \beta - A \geq 0\) 且 \(r_y + \beta - A \geq 0\)。由于 \(r_x > r_y\)，条件简化为 \(A \leq r_y + \beta\)。

2. 双方都不买是均衡，当且仅当：\(r_x - A \leq 0\) 且 \(r_y - A \leq 0\)。条件为 \(A \geq r_x\)。

3. 只有 Xena 购买是均衡，当且仅当：\(r_x - A \geq 0\)（Xena 愿意单独购买）且 \(r_y + \beta - A \leq 0\)（Yuri 即使加入也不划算）。条件为 \(r_y + \beta \leq A \leq r_x\)，这要求 \(\beta < r_x - r_y\)。

4. 只有 Yuri 购买不可能成为均衡，因为这要求 \(r_x + \beta \leq A \leq r_y\)，与 \(r_x > r_y\) 矛盾。

两种情形的分叉

根据网络效应的强度，市场呈现不同特征：

情形一：弱网络效应（\(\beta < r_x - r_y\)）

弱网络效应下的需求曲线

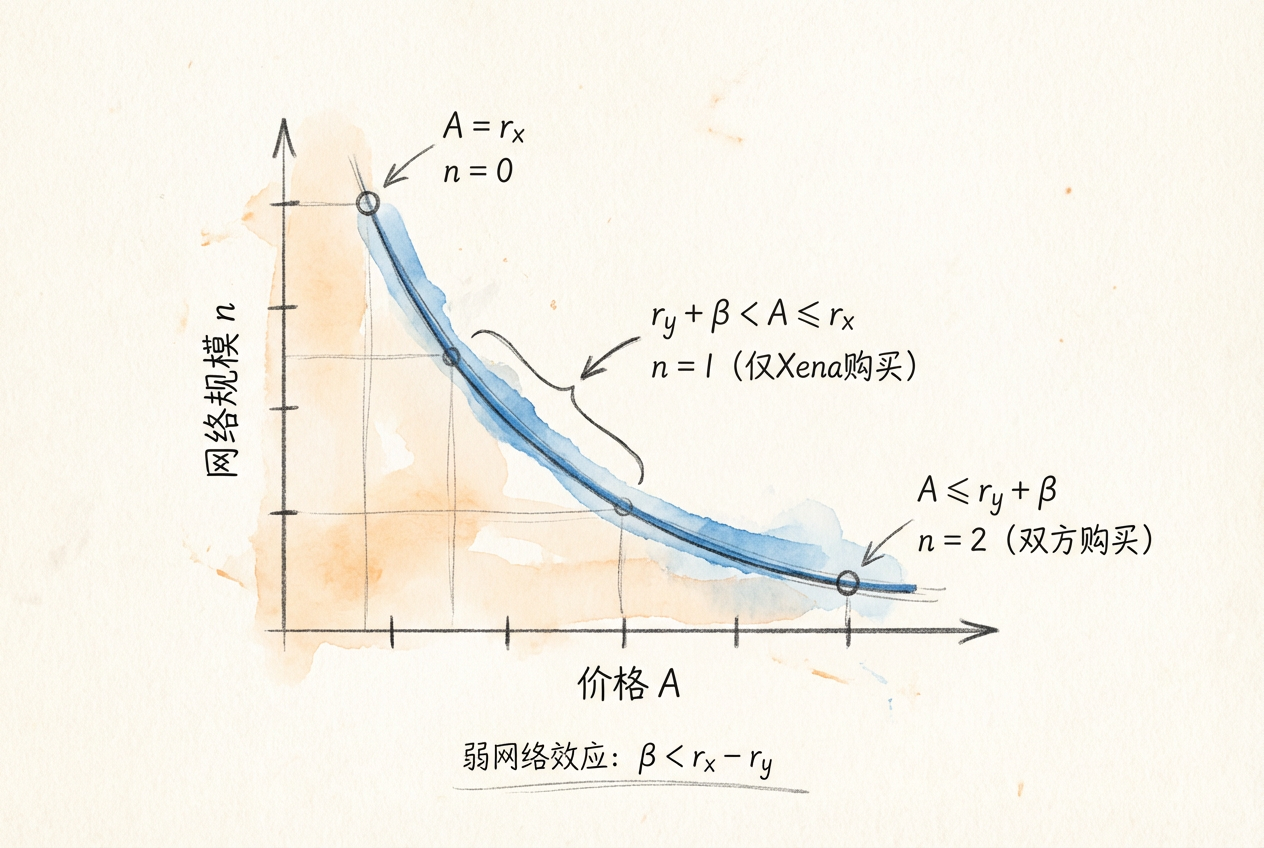
当网络收益较小或用户异质性较大时，每个价格对应唯一的需求量： - \(A > r_x\)：无人购买 - \(r_y + \beta < A \leq r_x\)：只有 Xena 购买 - \(A \leq r_y + \beta\)：双方都购买

这与传统需求曲线类似——价格越低，需求越高。

情形二：强网络效应（\(\beta > r_x - r_y\)）

强网络效应下的需求曲线

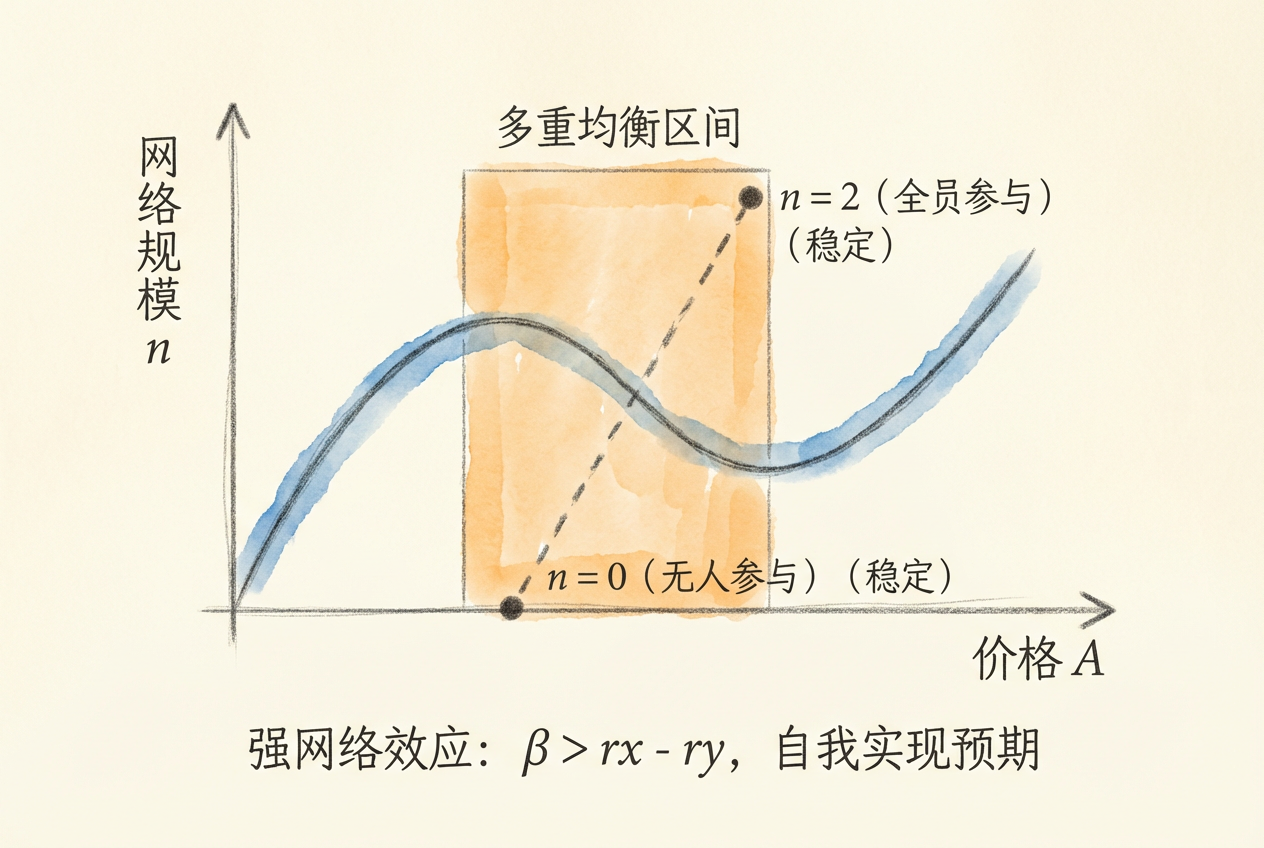
当网络收益足够大时，情况发生质变。不存在只有一人购买的均衡，但在 \(r_x \leq A \leq r_y + \beta\) 的价格区间内，「双方都买」和「双方都不买」同时是均衡！

这意味着：同一价格可以对应多个需求水平。最终市场走向哪个结果，取决于用户的预期。

重要核心发现 3.1

网络效应使用户的购买决策相互依赖。当网络效应足够强时，同一价格可能对应多个需求水平，形成多重均衡。市场的最终状态取决于用户的预期——这就是自我实现预期（Self-Fulfilling Expectations）的机制。

自我实现预期的直觉

假设价格 \(A = (r_x + r_y + \beta)/2\)，处于多重均衡区间。

如果双方都相信对方会买，他们会计算：加入网络的净收益 = 内在估值 + 网络收益 - 价格。由于预期对方会买，网络收益可以实现，双方都发现购买是值得的。于是预期得到验证。

反之，如果双方都相信对方不会买，他们会计算：单独购买的净收益 = 内在估值 - 价格。没有网络收益，双方都发现价格太高，于是都不买。悲观的预期同样得到验证。

两种预期都可以自我实现——这是协调博弈的本质特征。

3.1.2 多用户需求分析

现实中用户数量远不止两个。让我们将模型扩展到连续统用户（Continuum of Users）。

模型设定

假设用户类型 \(r\) 在 \([0, 1]\) 上均匀分布，代表用户对产品内在价值的估值。所有用户共享相同的网络效应强度 \(\beta\)。用户 \(r\) 加入网络的效用为：

\[u = r + \beta n^e - A\]

其中 \(n^e\) 是用户对网络规模的预期。

满足预期均衡

在满足预期均衡（Fulfilled-Expectations Equilibrium, FEE）中，用户的预期与实际结果一致，即 \(n = n^e\)。

临界用户类型 \(r_0\) 满足：\(r_0 + \beta n^e - A = 0\)，即 \(r_0 = A - \beta n^e\)。

所有 \(r \geq r_0\) 的用户会加入网络，因此网络规模为 \(n = 1 - r_0 = 1 - A + \beta n^e\)。

在满足预期均衡中，\(n = n^e\)，解得：

\[n = \frac{1 - A}{1 - \beta} \quad \text{（当 } 0 < n < 1 \text{ 时）}\]

多用户模型中的需求曲线

关键分叉点：\(\beta = 1\)

• 当 \(\beta < 1\)：每个价格对应唯一的网络规模，需求函数单调递减。
• 当 \(\beta > 1\)：对于某些价格区间，存在三个满足预期均衡——零网络、小网络和大网络。

异质网络收益模型（Rohlfs 模型）

另一种建模方式是假设用户对网络收益的估值不同。设 \(\beta \sim U[0, 1]\)，所有用户共享相同的内在估值 \(r\)。用户效用为 \(r + \beta n^e - A\)。

通过类似分析，我们得到逆需求函数：

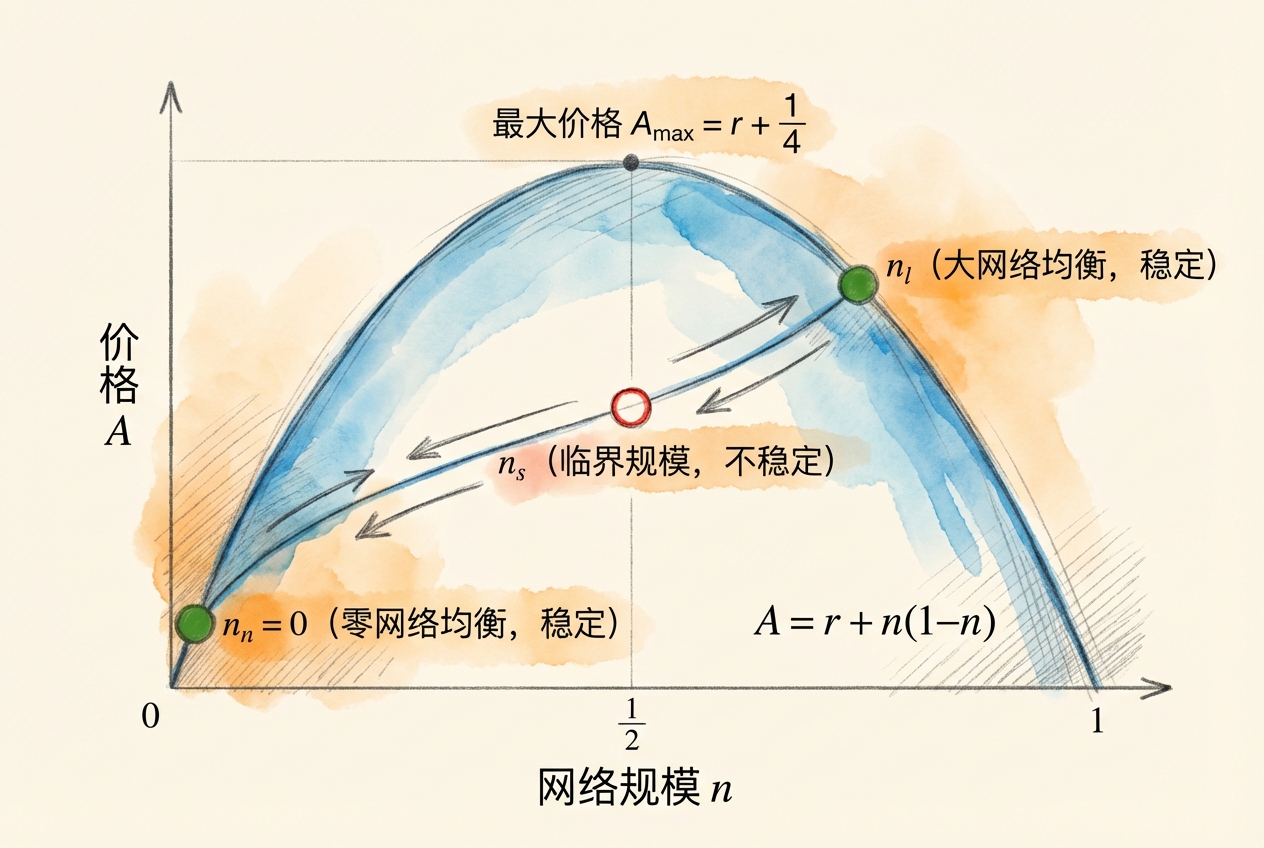
\[A = r + n(1 - n)\]

这是一个倒 U 形函数！在 \(n = 1/2\) 处达到最大值 \(A_{\max} = r + 1/4\)。

为什么是倒 U 形？

这里有两股力量在博弈： - 需求法则：价格上升应该减少需求 - 网络效应：更大的预期网络规模提高支付意愿

对于小网络（\(n < 1/2\)），网络效应占主导，价格可以随网络规模上升；对于大网络（\(n > 1/2\)），需求法则占主导，价格随网络规模下降。

这意味着：对于 \(r < A < r + 1/4\)，存在三个均衡网络规模：

\[n_n = 0, \quad n_s = \frac{1}{2} - \frac{1}{2}\sqrt{1 - 4(A-r)}, \quad n_l = \frac{1}{2} + \frac{1}{2}\sqrt{1 - 4(A-r)}\]

重要核心发现 3.2

当网络效应足够强时，需求曲线可能存在上升区间——更高的需求对应更高的价格。这导致同一价格可能对应最多三个均衡需求水平（包括零需求），其中每一个都是自我实现的预期。

3.1.3 预期形成与均衡稳定性

并非所有满足预期均衡都是稳定的。我们引入动态分析来筛选均衡。

近视动态

假设用户采用近视预期（Myopic Expectations）：他们基于当前网络规模决策，但不预测自己的决策对未来规模的影响。

设 \(t\) 期网络规模为 \(n_t\)，用户预期 \(n^e = n_t\)。基于此预期，实际加入网络的用户形成 \(t+1\) 期的网络规模 \(n_{t+1}\)。

设 \(n(n^e)\) 为基于预期 \(n^e\) 形成的实际网络规模函数。在 Rohlfs 模型中，当 \(A > r\) 且 \(n^e > A - r\) 时：

\[n(n^e) = 1 - \frac{A - r}{n^e}\]

我们计算：

\[n_{t+1} - n_t = n(n_t) - n_t = \frac{1}{n_t}(n_t - n_s)(n_l - n_t)\]

满足预期均衡的稳定性分析

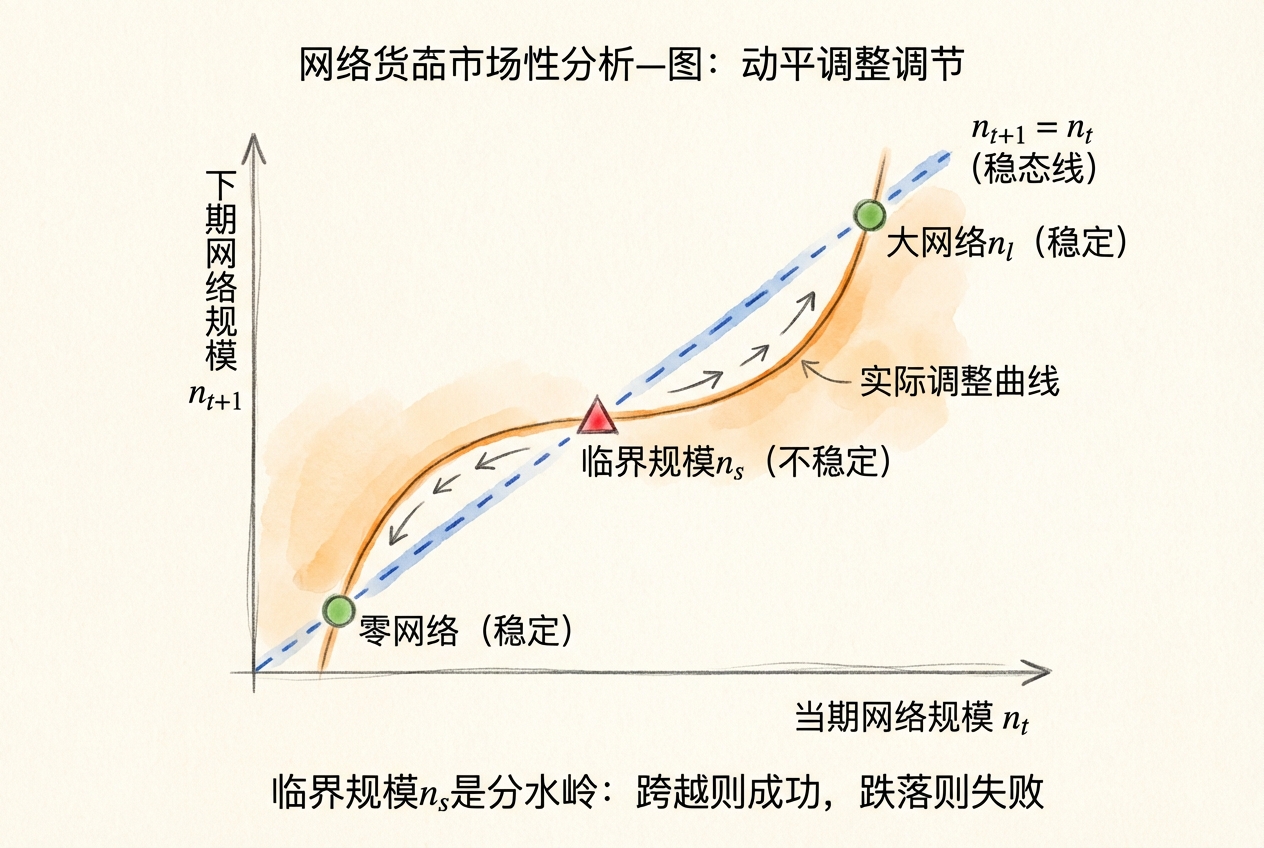
稳定性结论

• 零网络均衡 \(n_n = 0\)：稳定。任何低于 \(n_s\) 的初始规模都会收缩到零。
• 小网络均衡 \(n_s\)：不稳定。任何偏离都会使网络要么继续收缩（向零），要么扩张（向 \(n_l\)）。
• 大网络均衡 \(n_l\)：稳定。偏离后会回归。

重要核心发现 3.3

「零网络」和「大网络」均衡是稳定的，而「小网络」均衡是不稳定的。小网络均衡的规模定义了临界规模（Critical Mass）——一旦网络规模超过这个门槛，网络会自动滚雪球式增长，直到达到稳定的大网络均衡。

临界规模的经济含义

临界规模的存在意味着： 1. 网络建设初期存在「死亡区」——如果无法跨越临界规模，网络必然失败 2. 一旦跨越临界规模，正反馈开始启动 3. 如何度过早期「死亡区」是平台创业的核心挑战

注记案例：百万美元主页

2005 年，英国学生 Alex Tew 创建了一个网站，将主页划分为 100 万个像素，每像素售价 1 美元。起初，这个网站毫无流量——谁会为一个无人访问的网站付费广告呢？

但 Alex 理解自我实现预期的机制。他让家人朋友购买最初几块像素，然后向媒体发布新闻稿，BBC 和科技网站进行了报道。这引发了用户的好奇心：越来越多的广告商购买像素，访问量上升，吸引更多广告商。最终，所有像素售罄，Alex 赚到了 100 万美元以上。

他成功地跨越了临界规模，启动了正反馈循环。

3.1 小结

本节我们建立了分析网络商品需求的博弈论框架。核心发现包括：

1. 网络效应使用户决策相互依赖，传统的独立决策分析不再适用
2. 强网络效应导致多重均衡，同一价格可能对应多个需求水平
3. 均衡的实现依赖用户预期的协调——乐观预期和悲观预期都可以自我实现
4. 动态稳定性分析揭示了临界规模的存在，这是网络建设的关键门槛

3.2 网络商品定价

理解了需求侧的特殊性后，我们转向供给侧：平台如何为网络商品定价？网络效应的存在使得定价决策变得更加复杂。

3.2.1 垄断平台定价

双用户模型中的定价

回到 Xena 和 Yuri 的模型。假设平台边际成本为 \(f\)，且 \(f < r_x\)（至少卖给 Xena 是有利可图的）。

弱网络效应情形（\(\beta < r_x - r_y\)）

平台面临两种选择： - 高价 \(A = r_x\)：只有 Xena 购买，利润 \(\pi_1 = r_x - f\) - 低价 \(A = r_y + \beta\)：两人都买，利润 \(\pi_2 = 2(r_y + \beta - f)\)

平台选择限制网络规模（只卖给 Xena）的条件是 \(\pi_1 > \pi_2\)，即：

\[\beta < r_x - r_y - \frac{1}{2}(r_x - f)\]

数值例子：设 \(r_x = 10, r_y = 6, f = 2\)。

• 垄断者只卖给 Xena：定价 \(A = 10\)，利润 \(\pi_1 = 10 - 2 = 8\)
• 垄断者卖给两人：定价 \(A = 6 + \beta\)，利润 \(\pi_2 = 2(6 + \beta - 2) = 8 + 2\beta\)

条件 \(\beta < r_x - r_y - \frac{1}{2}(r_x - f) = 10 - 6 - 4 = 0\) 表明在此参数下，只要 \(\beta > 0\)，卖给两人总是更优。例如当 \(\beta = 1\) 时，\(\pi_2 = 10 > \pi_1 = 8\)。这说明网络收益足够强时，垄断者会服务整个市场。

而从社会福利角度，让两人都买更优的条件是总福利更高，即：

\[r_x + r_y + 2\beta - 2f > r_x - f \quad \Rightarrow \quad \beta > \frac{1}{2}(f - r_y)\]

关键观察：存在参数使得垄断者限制网络规模，但这种限制是对社会有害的。

强网络效应情形（\(\beta > r_x - r_y\)）

中间价格导致多重均衡。平台无法确定用户会协调到哪个均衡。 - 悲观平台选择 \(A = r_x\)，保证两人都买，利润 \(2(r_x - f)\) - 乐观平台选择 \(A = r_y + \beta\)，如果用户协调成功，利润更高：\(2(r_y + \beta - f)\)

警告注意

强网络效应下的定价决策本质上是对用户协调能力的赌博。平台需要评估用户达成乐观均衡的可能性。这为平台的预期管理策略提供了空间——通过各种手段引导用户形成乐观预期。

3.2.2 连续用户模型的定价

考虑纯网络商品：内在估值 \(r = 0\)，用户对网络效应的估值 \(\beta \sim U[0, 1]\)。逆需求函数为 \(A = n(1 - n)\)。

垄断定价

假设平台直接选择网络规模 \(n\)，成本函数 \(f(n)\)。利润为：

\[\Pi = n \cdot A - f(n) = n^2(1-n) - f(n)\]

注记模型假设的局限性

这里我们假设平台可以直接选择网络规模，这是一个强假设。现实中，平台只能设定价格，而网络规模由用户的协调结果决定。在存在多重均衡时，价格设定和规模选择并不等价——同一价格可能对应多个网络规模。本节的分析揭示了理想情形下的基准结果，实际定价决策更为复杂。

一阶条件给出垄断规模 \(n^m\)：\(n(2 - 3n) = f'(n)\)

完全竞争

在完全竞争下，价格等于边际成本，网络规模 \(n^c\) 满足：\(n(1 - n) = f'(n)\)

社会最优

总剩余为：

\[TS = \int_{1-n}^{1} \beta n \, d\beta - f(n) = \frac{1}{2}n^2(2 - n) - f(n)\]

社会最优规模 \(n^*\) 满足：\(\frac{n(4 - 3n)}{2} = f'(n)\)

垄断、完全竞争与社会最优的网络规模比较

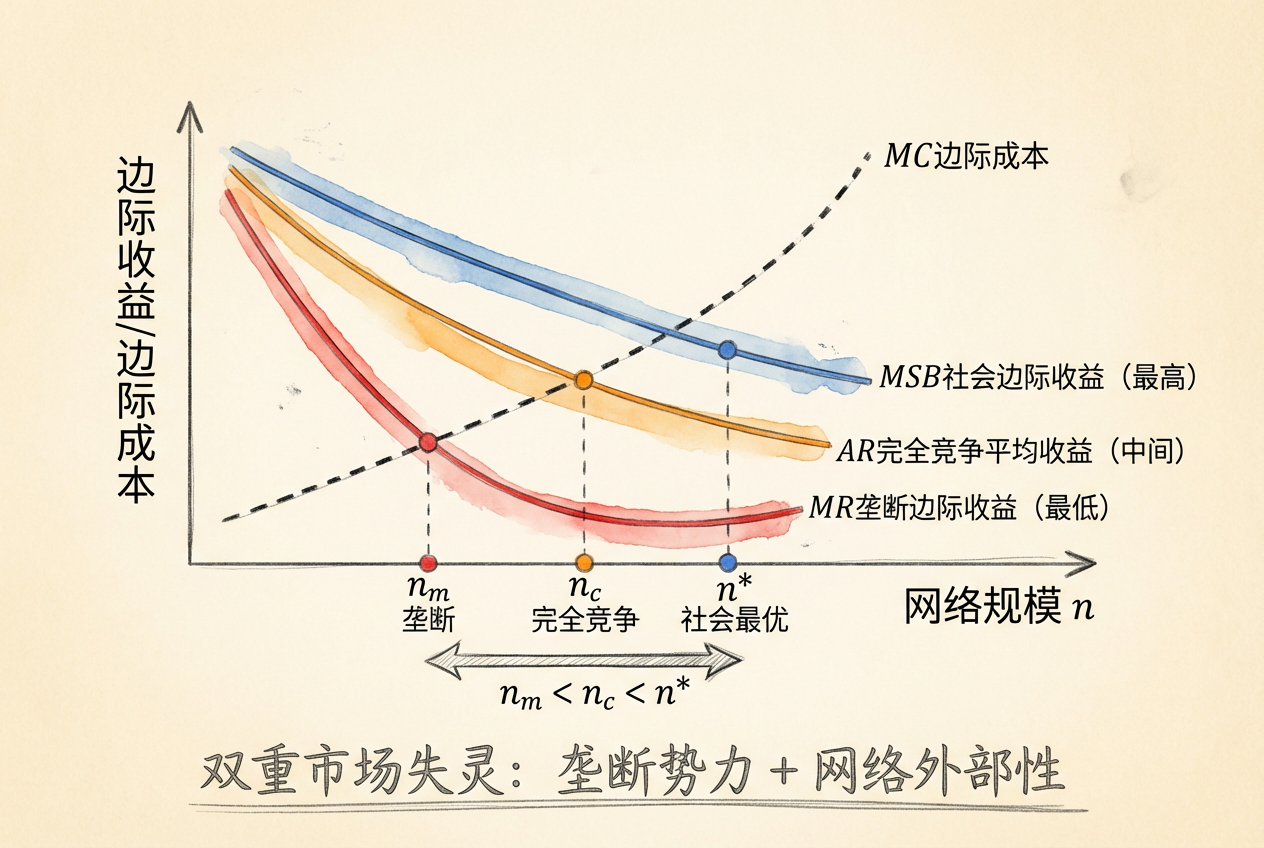
核心结论

当边际成本不太高时（\(f'(1/2) \leq 1/4\)），有：

\[n^m < n^c < n^*\]

重要核心发现 3.4

垄断者倾向于支持较小的网络规模并收取较高的价格，这与传统垄断分析一致。但更重要的发现是：即使在完全竞争下，网络规模也低于社会最优。这是因为用户加入网络时，只考虑自己获得的网络收益，而不考虑自己的加入给其他用户带来的额外收益——这是典型的正外部性。

网络商品市场存在双重市场失灵： 1. 垄断势力：平台限制产量以提高价格 2. 网络外部性：用户不内化对其他用户的正外部性

3.2.3 存在替代网络时的定价

现实中往往存在替代选择。我们用 Hotelling 模型分析这种情况。

模型设定

新平台位于 0，老网络位于 1，用户均匀分布在 \([0, 1]\) 区间上。用户 \(x\) 的效用为：

\[U(x) = \begin{cases} r + q - \tau x + \beta_1 n_1^e - A_1 & \text{加入新平台} \\ r - \tau(1-x) + \beta_2 n_2^e & \text{留在老网络（免费）} \end{cases}\]

其中 \(q\) 是新平台的质量优势，\(\tau\) 是单位距离的「运输成本」（代表用户偏好异质性）。

无差异用户 \(x_0\) 满足加入新平台和留在旧网络的效用相等：

\[r + q - \tau x_0 + \beta_1 n_1^e - A_1 = r - \tau(1-x_0) + \beta_2 n_2^e\]

整理得：

\[q - \tau x_0 + \beta_1 n_1^e - A_1 = -\tau + \tau x_0 + \beta_2 n_2^e\]

\[2\tau x_0 = \tau + q + \beta_1 n_1^e - \beta_2 n_2^e - A_1\]

因此无差异用户位置为：

\[x_0 = \frac{1}{2} + \frac{q + \beta_1 n_1^e - \beta_2 n_2^e - A_1}{2\tau}\]

在满足预期均衡中，\(n_1 = x_0\)，\(n_2 = 1 - x_0\)，解得：

\[n_1 = \frac{q + \tau - \beta_2 - A_1}{2\tau - \beta_1 - \beta_2}\]

需求的走向取决于网络效应强度

• 弱网络效应（\((\beta_1 + \beta_2)/2 < \tau\)）：需求向下倾斜，每个价格对应唯一需求，市场存在两个网络共存的空间。
• 强网络效应（\((\beta_1 + \beta_2)/2 > \tau\)）：需求可能向上倾斜，多重均衡可能出现，市场可能「倾覆」（Tipping）到只剩一个网络。

重要核心发现 3.5

当平台面临竞争网络时，市场结构取决于两股力量的平衡：产品差异化使用户倾向分散选择，网络效应驱动用户集中到同一平台。产品差异化更强时，两个网络可以共存；网络效应更强时，市场可能倾覆到单一网络主导。

弱网络效应下的最优定价

新平台最大化利润 \(\pi_1 = A_1 \cdot n_1\)，最优价格：

\[A_1^* = \frac{q + \tau - \beta_2}{2}\]

网络规模：

\[n_1^* = \frac{q + \tau - \beta_2}{2(2\tau - \beta_1 - \beta_2)}\]

利润：

\[\pi_1^* = \frac{(q + \tau - \beta_2)^2}{4(2\tau - \beta_1 - \beta_2)}\]

有趣的比较静态：当老网络的网络效应 \(\beta_2\) 增强时，新平台会降低价格。如果新平台自身网络效应够强（\(\beta_1 > \tau - q\)），这种降价甚至可能导致市场份额上升！

注记案例：微信支付 vs 支付宝

2014 年，支付宝占据移动支付市场 82% 的份额，看起来已形成垄断。但微信支付通过春节红包成功启动，迅速打破了这一格局。

从本节模型看： - 支付宝是「老网络」，拥有庞大的用户基础和商户覆盖 - 微信支付是「新平台」，质量优势 \(q\) 来自社交场景的无缝整合 - 红包活动本质上是渗透定价——通过补贴跨越临界规模

微信支付的成功说明：即使面对强大的在位者，如果新进入者能够找到差异化的场景（社交支付 vs 电商支付），并通过有效的临界规模策略启动正反馈，仍然可以打破既有格局。

到 2024 年，两者形成了稳定的双寡头格局：支付宝主导电商场景（83%），微信支付主导线下小额高频场景（63%）。这种场景分化的共存，正是「弱网络效应」情形的典型体现——产品差异化足以支撑两个网络共存。

3.2 小结

本节分析了网络商品的定价决策，主要发现：

1. 垄断平台可能限制网络规模以提高价格，损害社会福利
2. 即使完全竞争也无法达到社会最优，因为用户不内化网络外部性
3. 面对竞争网络时，价格策略取决于网络效应与产品差异化的相对强度
4. 强网络效应可能导致市场倾覆，弱网络效应允许多网络共存

3.3 网络效应管理策略

网络效应的存在使得平台竞争变成了一场「标准之战」。本节讨论平台的三类核心策略：兼容性决策、动态定价和先发优势的利用。

3.3.1 兼容性决策

兼容性（Compatibility）决定了不同网络的用户能否相互连通。这是平台最重要的战略决策之一。

兼容性的双重效应

选择兼容有两个效应：

1. 扩大网络效应：兼容使所有用户可以互联，形成一个「全局」大网络，提高所有用户的支付意愿
2. 消除内生质量差异：兼容后，网络规模不再是竞争优势，只剩下内在质量的竞争

模型分析

沿用上一节的 Hotelling 模型，假设 \(\beta_1 = \beta_2 = \beta < \tau\)（弱网络效应）。

不兼容时（前面已分析）：利润 \(\pi_1^* = \frac{(q + \tau - \beta)^2}{8(\tau - \beta)}\)

兼容时：所有用户都能互联，\(n_1^e = n_2^e = 1\)。无差异用户：

\[x_0 = \frac{\tau + q - A_1}{2\tau}\]

最优价格 \(A_1^c = \frac{\tau + q}{2}\)，利润：

\[\pi_1^c = \frac{(\tau + q)^2}{8\tau}\]

平台的兼容性选择

比较两种情形的利润：

\[\pi_1^c - \pi_1^* = \beta \frac{\tau^2 - \beta\tau - q^2}{8\tau(\tau - \beta)}\]

令 \(\hat{q} = \sqrt{\tau(\tau - \beta)}\)，则： - 当 \(q < \hat{q}\)：平台偏好兼容 - 当 \(q > \hat{q}\)：平台偏好不兼容

重要核心发现 3.6

拥有较小质量优势的平台倾向于选择兼容，因为兼容提高了用户支付意愿。拥有较大质量优势的平台倾向于选择不兼容，因为不兼容使其可以利用网络规模优势。然而，平台选择不兼容时可能损害用户利益——用户通常偏好兼容带来的更大网络。

兼容性决策分析矩阵

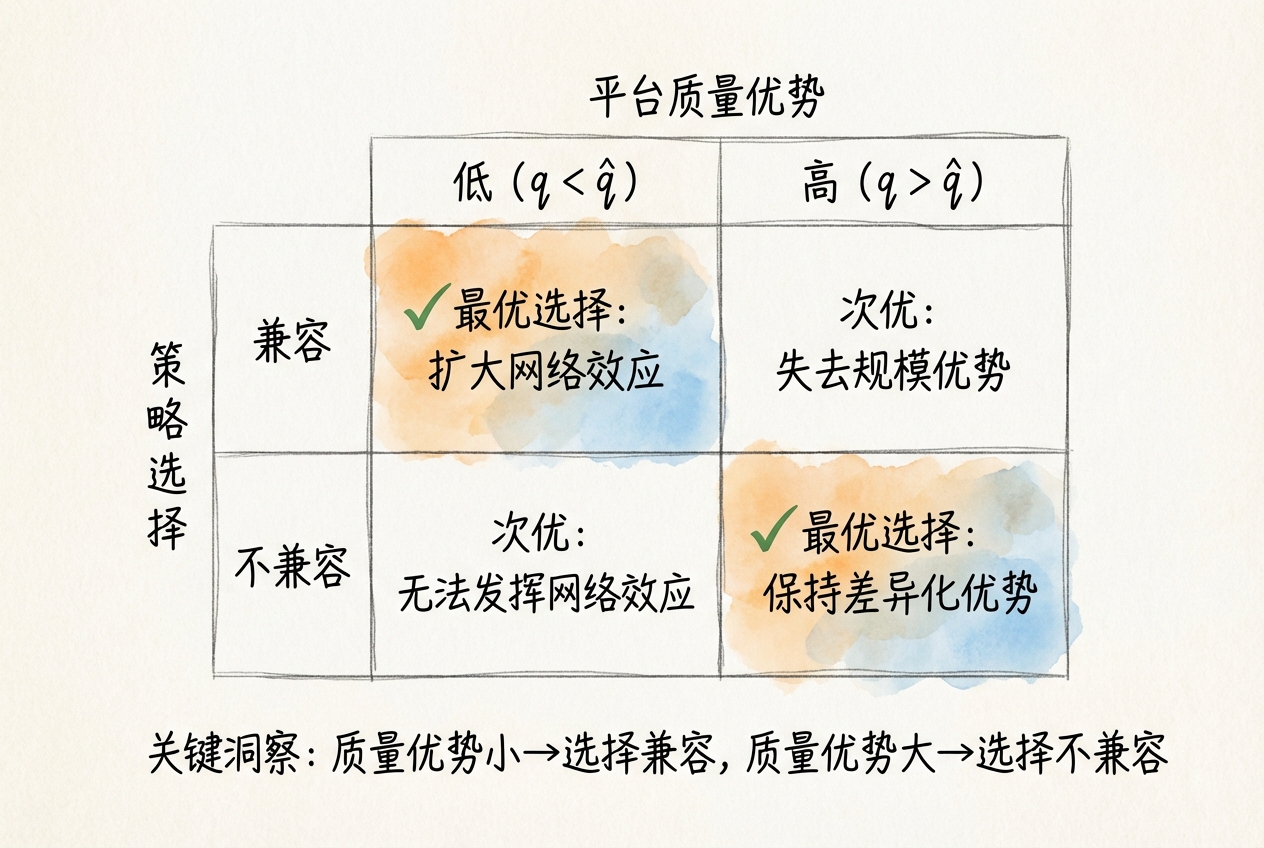
用户偏好与平台偏好的冲突

分析表明，当 \(\tau > (9/8)\beta\) 时，在 \(q = \hat{q}\) 附近，平台选择不兼容会损害用户福利。这为监管干预提供了理论依据——政府可能需要强制要求互操作性。

注记案例：鸿蒙 OS 的兼容性策略

华为鸿蒙 OS 的演进完美诠释了兼容性决策的动态逻辑：

2019-2023年：兼容策略 - 美国制裁迫使华为加速自研操作系统 - 初期鸿蒙完全兼容 Android 应用，降低用户转换成本 - 此时鸿蒙是「新平台」，质量优势 \(q\) 较小，选择兼容符合理论预测

2024年起：不兼容策略 - 鸿蒙 NEXT 宣布完全移除 Android 代码 - 生态日趋成熟，5000+ 应用完成原生开发 - 此时鸿蒙已建立差异化优势（跨设备协同），\(q\) 增大，开始转向不兼容

这一策略转变与理论预测一致：新进入者初期选择兼容以降低壁垒，建立规模后转向不兼容以建立差异化优势。

到 2024 年 Q4，鸿蒙在中国市场份额达到 19%，首次超越 iOS 成为第二大移动操作系统（数据来源：Counterpoint Research，2024 年 12 月）。

3.3.2 动态定价

静态模型无法捕捉平台竞争的动态本质。实际上，平台需要在「收割」当前优势和「投资」未来规模之间权衡。

收割 vs 投资的两难

领先的平台面临： - 收割诱惑：利用当前的大网络优势，收取高价 - 投资诱惑：继续低价扩大网络，巩固长期优势

这两种激励方向相反，最优策略取决于贴现率、网络效应强度和用户更新率。

渗透定价

渗透定价（Penetration Pricing）是网络商品市场的常见策略：早期收取低价甚至补贴用户，以跨越临界规模；一旦建立规模优势，再逐步提高价格。

临界规模与市场倾覆机制

注记案例：共享单车大战与临界规模

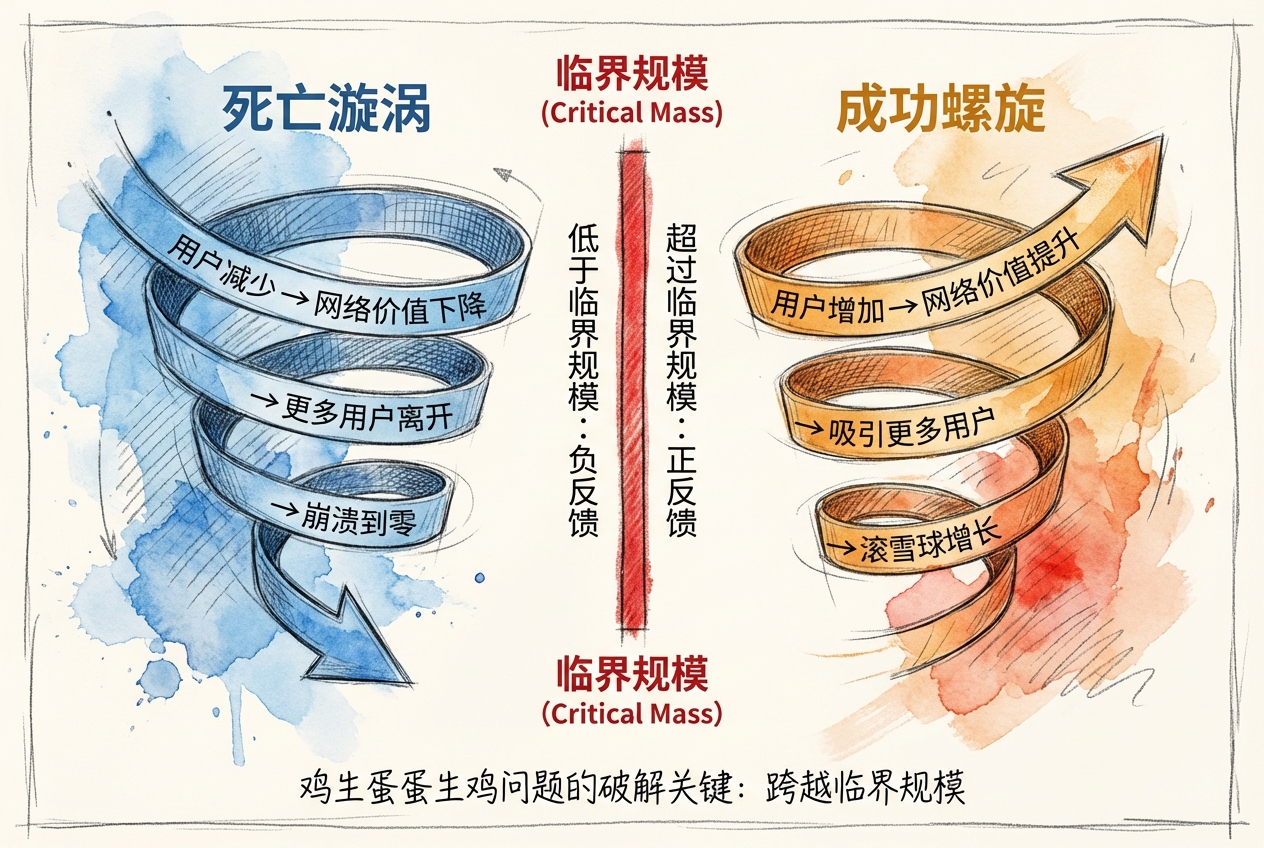
2016-2018 年中国共享单车市场是临界规模失败的教科书案例。

ofo 的错误： - 以为全国用户总量是临界规模的衡量标准 - 22 亿美元融资主要用于全国铺车和补贴大战 - 忽视了共享单车网络效应的局部性——需要在每个城市达到足够密度

结果： - 同时在全国建立「小网络」，无一城市真正达到临界规模 - 用户体验差（车辆损坏率高、找车困难）导致预期恶化 - 预期恶化加速崩溃——这正是「不稳定均衡」滑向「零网络均衡」的过程

哈啰的逆袭： - 聚焦二三线城市，单城市精细化运营 - 先在有限区域达到临界密度，再逐步扩张 - 资源有限反而促使正确识别临界规模的边界

教训：临界规模是局部概念。对于具有地理局限性的网络效应，盲目全国扩张可能适得其反。

3.3.3 先发优势

网络效应使得先发优势（First-Mover Advantage）尤为重要。先发者可以： - 建立安装基础 - 影响用户预期 - 锁定早期用户

但先发优势并非绝对。以下因素可能削弱它：

内在质量的作用

后发者可能拥有更好的产品。正如 Hagiu 和 Rothman 观察：「成功的平台往往不是最先进入市场的，而是最先创造流动性的。」Airbnb 晚于 VRBO 十年，阿里巴巴是中国 eBay 的后来者，Uber 的 UberX 模式实际上是学习 Lyft。

向后兼容的束缚

先发者可能被旧版本束缚。为了维护向后兼容性，他们难以进行激进的产品升级。后发者可以从零开始设计更优的产品。

预期管理

如果用户预期形成不完全理性，平台可以通过产品预告（Product Preannouncement）等手段影响预期。但这是一把双刃剑——可能冻结竞争对手的销售，也可能冻结自己当前产品的销售。

警告标准战争的历史教训

VHS vs Betamax 是标准战争的经典案例。技术上，Betamax 被认为画质更好。但 JVC 的 VHS 采取了更开放的授权策略，吸引更多厂商加入，更快地建立了安装基础。当 VHS 的网络规模优势形成后，即使 Betamax 技术更好，也无法逆转局面。

这说明：在网络商品市场，速度和规模可能比技术质量更重要。但这并不意味着技术不重要——它只是说明了跨越临界规模的紧迫性。

3.3 小结

本节讨论了网络效应管理的三类核心策略：

1. 兼容性决策：质量优势小的平台倾向兼容，质量优势大的平台倾向不兼容，但这可能损害用户利益
2. 动态定价：平台需在「收割」和「投资」间权衡，渗透定价是跨越临界规模的常用策略
3. 先发优势：网络效应放大先发优势，但内在质量、向后兼容和预期管理可能逆转局面

本章小结

本章建立了分析网络效应的基本理论框架，主要发现如下：

重要核心要点

1. 需求的相互依赖：网络效应使用户决策相互依赖，形成协调博弈结构。每个用户的购买决策取决于对其他用户行为的预期。

2. 多重均衡与自我实现预期：强网络效应导致多重均衡——同一价格可能对应多个需求水平。乐观预期和悲观预期都可以自我实现。

3. 临界规模：不稳定的「小网络」均衡定义了临界规模。一旦跨越这个门槛，网络会滚雪球式增长到稳定的「大网络」均衡。

4. 双重市场失灵：垄断势力和网络外部性共同导致网络规模低于社会最优。即使在完全竞争下，用户也不会内化对其他用户的正外部性。

5. 兼容性决策：拥有质量优势的平台倾向不兼容，但这可能损害用户福利。监管者可能需要干预以促进互操作性。

这些理论洞见为后续章节的分析奠定了基础：

• 第 4 章将分析平台如何度过启动阶段，解决「鸡生蛋蛋生鸡」问题
• 第 5 章将深入探讨双边市场的定价策略
• 第 6 章将讨论平台设计如何影响网络效应的实现
• 第 7 章将分析网络效应对竞争政策的影响

思考题

概念理解

1. 解释为什么同一价格可能对应多个需求水平。这种现象在什么条件下会出现？

2. 什么是满足预期均衡（FEE）？为什么我们在分析网络商品市场时要求预期被满足？

模型应用

3. 考虑两个用户的模型，设 \(r_x = 10\)，\(r_y = 6\)，\(\beta = 3\)，边际成本 \(f = 2\)。
   • 这属于弱网络效应还是强网络效应情形？
   • 分析所有可能的纳什均衡
   • 计算垄断平台的最优定价策略和利润
4. 在 Rohlfs 模型中，设 \(r = 0.1\)，\(A = 0.2\)。
   • 计算三个满足预期均衡的网络规模
   • 分析哪些均衡是稳定的，为什么？
   • 临界规模是多少？

案例分析

5. 分析微信支付如何在支付宝占据 82% 市场份额的情况下成功突围。结合本章理论，讨论：
   • 微信红包如何帮助跨越临界规模？
   • 社交场景与电商场景的分化如何支撑双寡头均衡？
6. 讨论鸿蒙 OS 从兼容 Android 到去 Android 化的策略转变。如果没有美国制裁这一外部冲击，鸿蒙能成功吗？

开放讨论

7. 从社会福利角度，移动支付市场的互联互通是否应该强制推行？讨论兼容性管制的利弊。

8. ofo 的失败和哈啰的成功给平台创业者什么启示？临界规模的「局部性」意味着什么？

延伸阅读

经典英文文献

• Katz, M. L., & Shapiro, C. (1985). Network externalities, competition, and compatibility. American Economic Review, 75(3), 424-440.
  • 网络外部性和兼容性决策的开创性论文
• Farrell, J., & Saloner, G. (1985). Standardization, compatibility, and innovation. Rand Journal of Economics, 16(1), 70-83.
  • 分析标准竞争中的协调问题和创新激励
• Cabral, L. (2011). Dynamic price competition with network effects. Review of Economic Studies, 78(1), 83-111.
  • 网络效应下动态定价竞争的理论模型
• Rohlfs, J. (1974). A theory of interdependent demand for a communications service. Bell Journal of Economics and Management Science, 5(1), 16-37.
  • 网络商品需求理论的早期经典
• Belleflamme, P., & Peitz, M. (2021). The Economics of Platforms: Concepts and Strategy. Cambridge University Press.
  • 本章内容的主要参考来源，特别是第 3 章